A teraz nie lada gratka dla wszystkich ósmoklasistów, czyli zadanie z geometrii. Rozwiążemy je w mgnieniu oka. Chcesz zobaczyć jak?
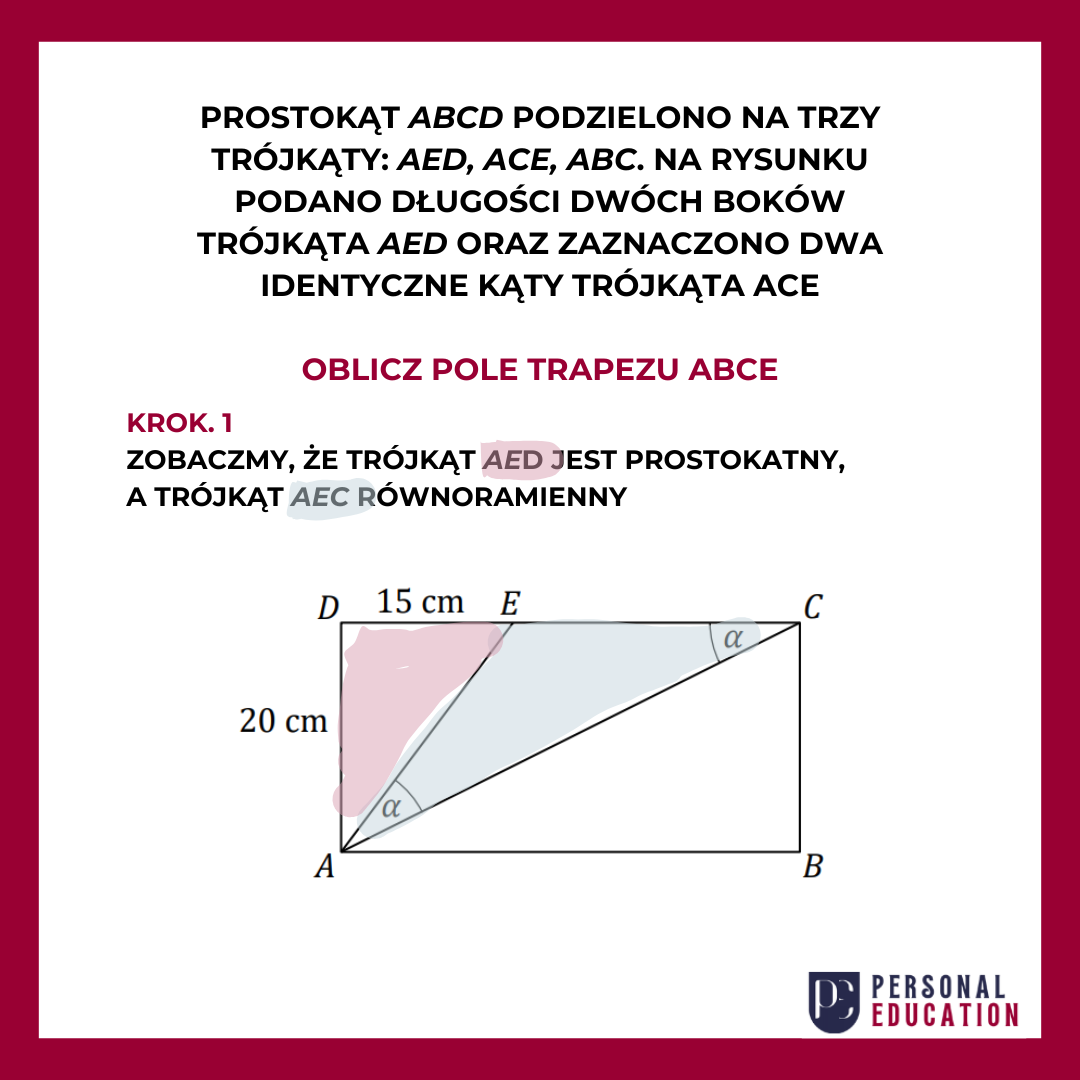
Zerknij na rysunek i zastanów się co widzisz. W środku prostokąta znalazły się trzy charakterystyczne trójkąty. Trójkąt ADE jest prostokątny, bo przy wierzchołku D jest kąt o mierze 90 stopni. Trójkąt ABC również, a kąt prosty znajduje się przy wierzchołku B. Trójkąt AEC natomiast to trójkąt równoramienny. Skąd to wiadomo? Wskazują na to dwa identyczne kąty zaznaczone na rysunku, które znajdują się przy wierzchołku A i przy wierzchołku C

Skoro już wiesz, że trójkąt ADE jest prostokątny, to na pewno od razu przychodzi ci na myśl Twierdzenie Pitagorasa. Dzięki niemu jesteś w stanie wyliczyć długość odcinka |AE|. By prawidłowo wykorzystać to twierdzenie musisz podnieść do drugiej potęgi dwa boki, które stoją bezpośrednio przy kącie prostym (15 i 20) oraz dodać je ze sobą. I ta suma, to długość trzeciego odcinka |AE|(na rysunku oznaczono go literką c) podniesiona do kwadratu. Z obliczeń wynika, że długość odcinka |AE| to 25.

Jak już wcześniej zostało powiedziane trójkąt AEC jest równoramienny, zatem skoro długość odcinka |AE| to 25, to długość odcinka |EC| również musi wynosić 25, bo są to ramiona trójkąta równoramiennego.

Przed tobą już tylko dwa bardzo sympatyczne kroki. Podpisz na rysunku pozostałe boki widocznych figur. Odcinek |BC| ma taką samą długość, jak odcinek |AD| (bo są to boki prostokąta). I tak samo odcinek |AB| jest tak samo długi, jak odcinek |CD|, czyli 40 (15+25)
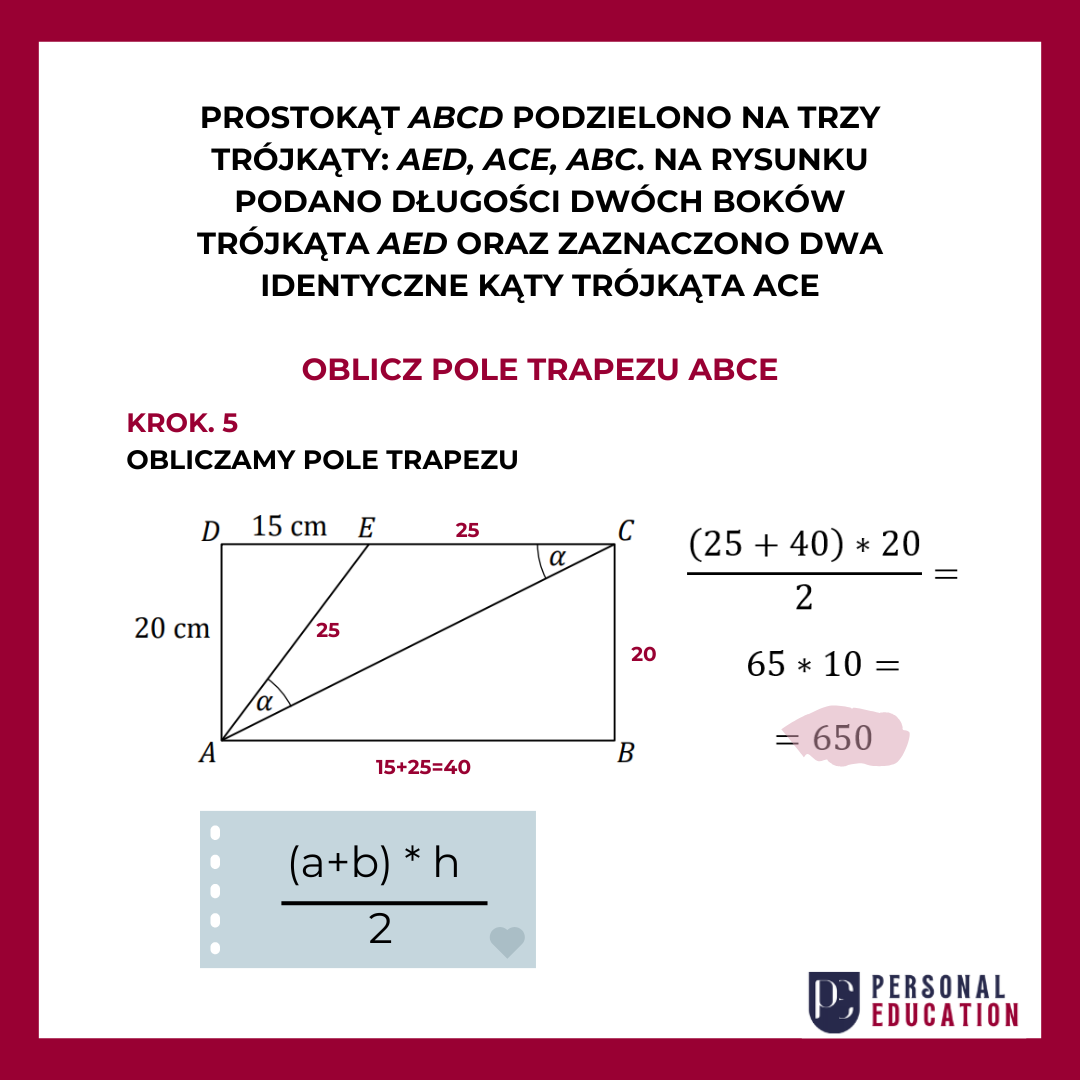
Juhu, masz już wszystkie elementy potrzebne do obliczenia pola trapezu ABCE. Dla przypomnienia wzór na pole trapezu widoczny jest w niebieskiej ramce. Dodajemy długości podstaw (czyli odcinki |CE| i |AB|), mnożymy razy wysokość (czyli odcinek |BC|) i dzielimy przez 2. Otrzymany wynik to 650. I jak? Udało się?



