Wielomiany, to zagadnienie, które bardzo często pojawia się w arkuszach maturalnych. Nie ma co zwlekać, naucz się je rozwiązywać, by nie dać się zaskoczyć na egzaminie! Przed tobą zadanie 9 z maja 2023 roku.

Na pierwszy rzut oka podany wielomian nie wygląda zbyt zachęcająco. Nic bardziej mylnego, bo zaraz zobaczysz, że może wyglądać lepiej.
Skorzystaj z metody grupowania, w której chodzi o to by wyciągnąć część wspólna przed wyrażenie. W tym przykładzie nasze dwie grupy zostały zaznaczone na różowo i fioletowo.

Gdy grupy są już lepiej widoczne wyciągnij część wspólną. Zawsze staraj się wyciągnąć najwięcej jak tylko się da. Co łączy 3x3-2x2? Oczywiście x2, dlatego to właśnie to wyrażenie postaw przed nawiasem, a wszystko to co pozostało wrzuć do środka nawiasu.
Wyciągając przed nawias dzielisz 3x3 przez x2, a wynik tego dzielenia zostawiasz w nawiasie. Tak samo postępujesz z -2x2, dzieląc przez x2 otrzymujesz -2. Pamiętaj by przy wszystkich obliczeniach znalazły się odpowiednie znaki (+ lub -)!
W identyczny sposób postępujesz z druga grupą, zaznaczoną na obrazku kolorem fioletowym.
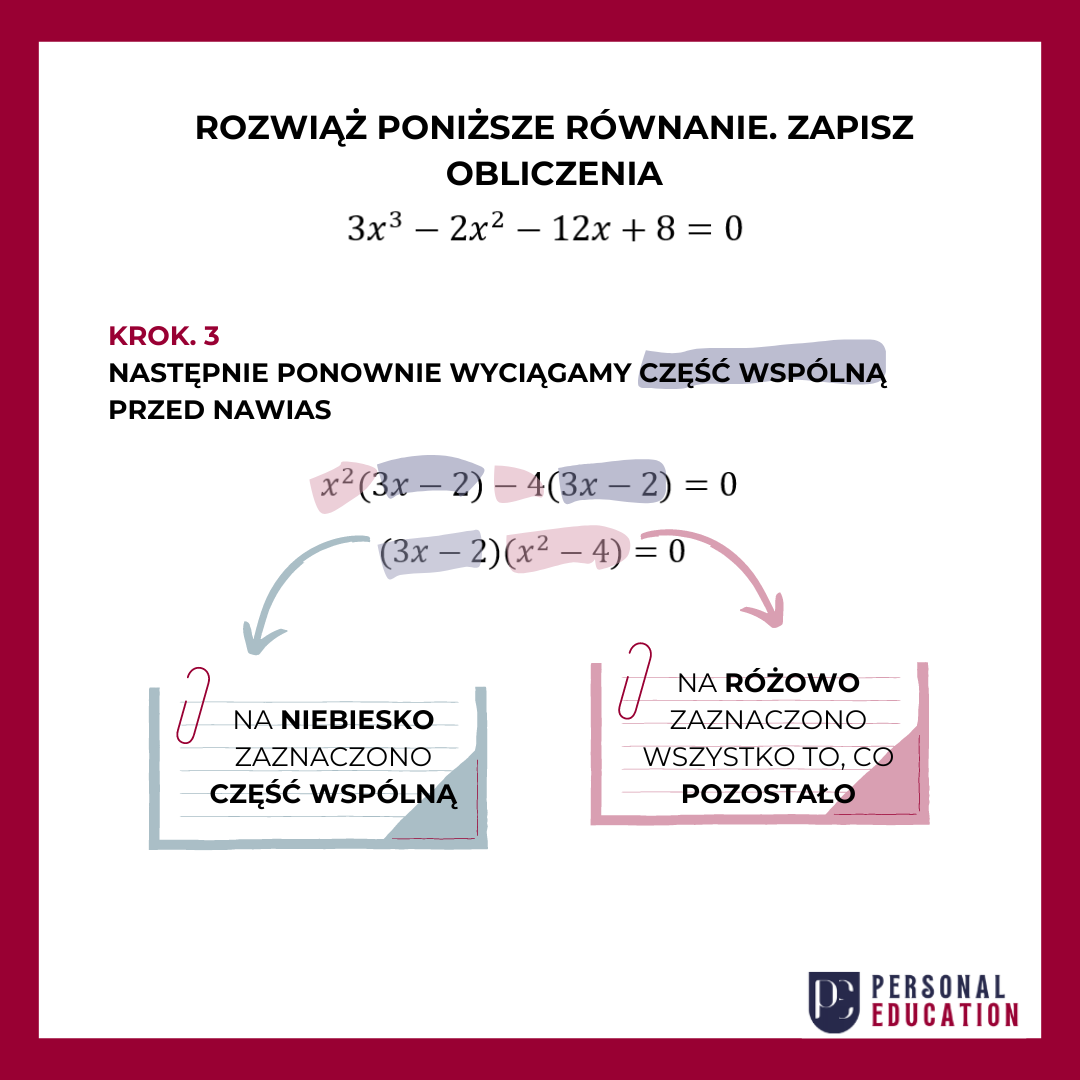
Zerknij na to co otrzymałeś. Czy któreś wyrażenia nie wyglądają podobnie, albo nawet identycznie? Nadeszła pora, byś znów wyciągnął je przed nawias!
Wyrażenie, które jest takie samo stawiasz na początku w jednym nawiasie, a do drugiego wrzucasz wszystko to, co pozostało. Prawda, że proste?

Przyjrzyj się dobrze wyrażeniu. Czy któryś z nawiasów nie przypomina wzoru skróconego mnożenia? Tak, oczywiście drugi nawias, u nas zaznaczony na fioletowo, to nic innego jak wzór: a2-b2=(a-b)(a+b). Wystarczy tylko go dobrze zastosować.
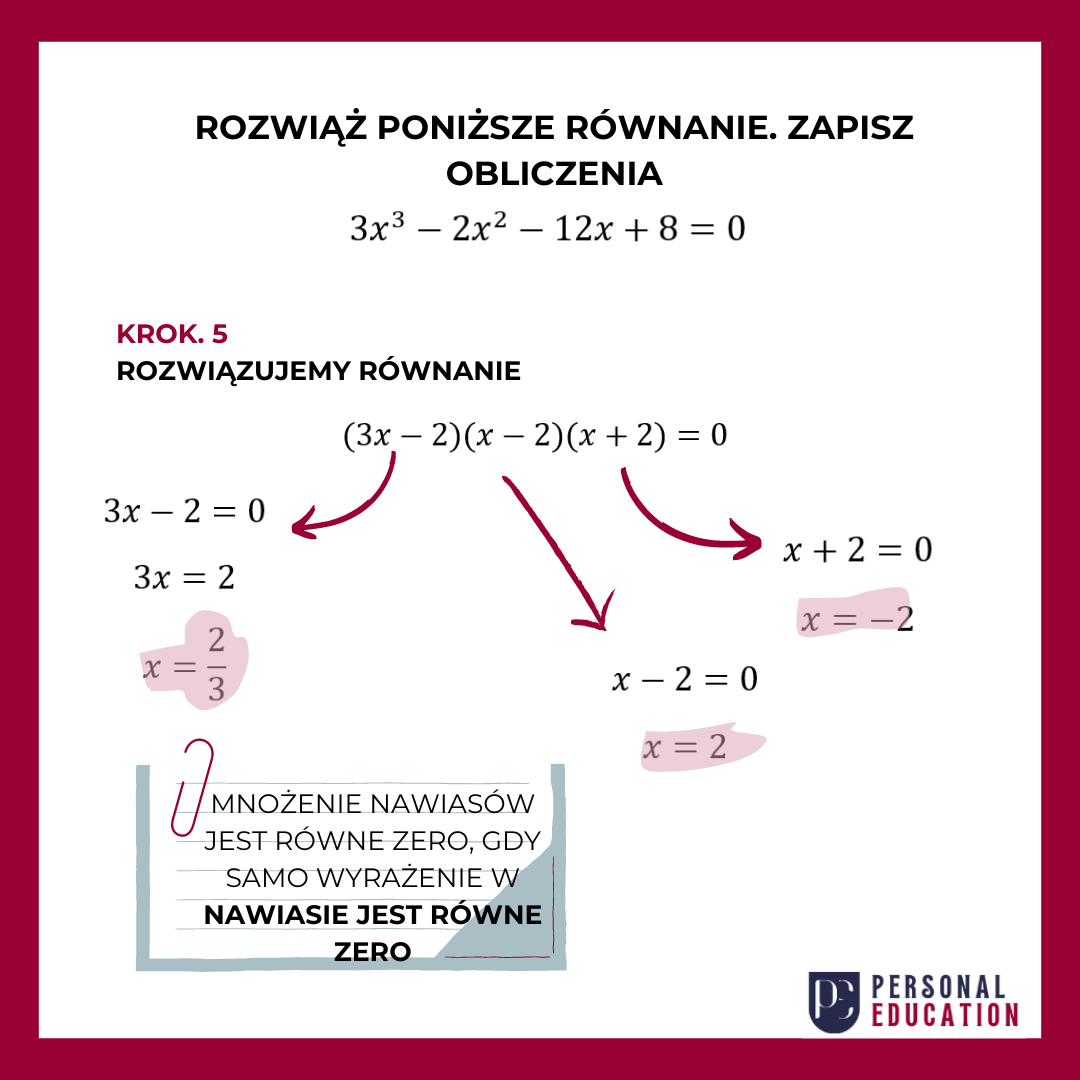
Masz przed sobą mnożenie trzech nawiasów, które daje wynik 0. Zatem wystarczy, że co najmniej jeden nawias będzie równy 0 i już masz skończone zadanie. Jak to sprawdzić? To co znajduje się w nawiasie musisz przyrównać do 0 i rozwiązać małe równanie, czyli znaleźć x. Tę czynność powtórz trzykrotnie (dla każdego nawiasu).

I to już koniec! Pozostało tylko zapisać wszystkie kroki, które wykonałeś i… gotowe!



